こんにちは。大宮校の宮下です。
毎年、西暦の数字にまつわる問題はよく出題されます。来年は2022年ですから、2022にまつわる問題が出題されることは予想できます。これを「2022問題」と呼ぶことにします。前回(11月1日)に2進数を取り上げましたが、0と2の2種類の数字を用いて数を表す変則2進数では2022は何番目になるでしょうか。
1番目⇒2
2番目⇒20
3番目⇒22
4番目⇒200
5番目⇒202
6番目⇒220
7番目⇒222
8番目⇒2000
9番目⇒2002
10番目⇒2020
11番目⇒2022
という具合に表記すると11番目であることがわかります。
また素因数分解すると、2022=2×3×337 となるので、2022は連続する3つの整数の和で表すことができます。
2022=673+674+675 これも使われそうですね。
さて、この対策として次の問題を考えてみましょう。
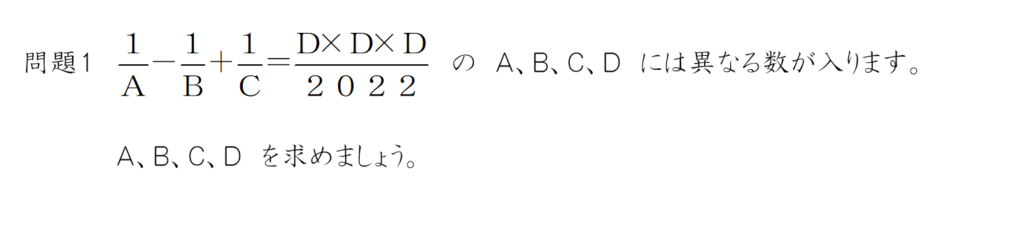
解説1 素因数分解すると、2022=2×3×337 となるので、これがA、B、Cになること
は、想像できますね。A=2 は確定です。
A=2、B=3、C=337 とすると、
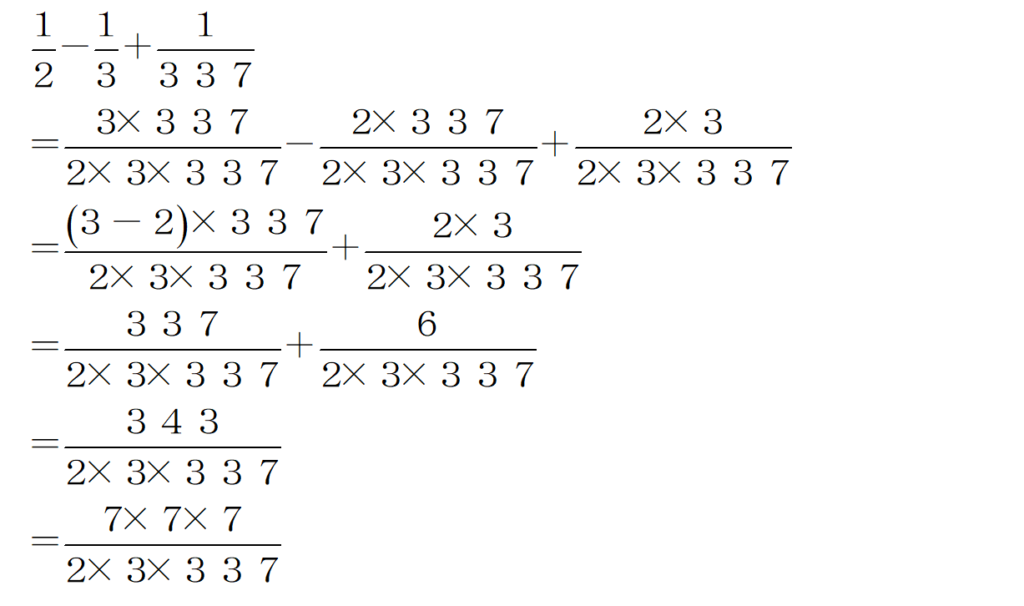
となり、D=7 になりますね。

解説2 2022を超えない最も大きい素数の平方数は、43×43=1849 ですね。
2022-1849=173 ですから 13×13=169 と 2×2=4 の和より
A=2、B=13、C=43 ですね。これ以外の組み合わせはなさそうです。
「2022」問題の対策として作問してみました。受験生の皆さんは、全力で頑張ってください。

