近年の難関中学入試算数では、いわゆる「やり方」を覚えていればできる問題は減少傾向にあります。一方で増えてきているのは、その場で情報整理をし、気づき、判断し、処理をしていくタイプの問題です。このような問題でも経験を重ねていくことで対応力は高まっていくのですが、練習した問題の答えを当てることを覚えても次の問題に残る経験は乏しく、学習の仕方に注意が必要です。
こういったタイプの問題を苦手とする生徒たちから上がるのが、自分たちは「ひらめき力」が無いから上手くいかないのだ…という声です。その是非に関してはいったん置いておきますが、その「ひらめき力」とはなんでしょうか?
例えば、有名な問題ですが、次の三角形の面積を求めることができます。
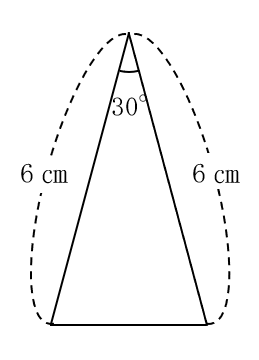
三角定規の性質を利用すると、底辺6cmに対して高さが3cmなので、
6×3÷2=9(cm2)です
では、次の三角形の面積は求められるでしょうか。
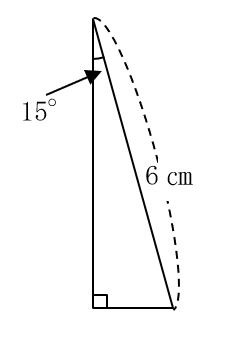
先ほどの二等辺三角形の半分なので(2つ合わせると先ほどの形になるので)、
9÷2=4.5(cm2)です
このことはひらめきと言えるほどのことではないですが、このように与えられた問題をそれよりも簡単な経験済みの問題に帰着させて考える力は非常に重要です。
では、この問題を次のように考えた場合はどうでしょうか。
1問目で30度のとき、高さが6cmの半分なので3cm
2問目は15度なので、角度が半分だから、さらに高さも半分で、3÷2=1.5(cm)
従って面積は、6×1.5÷2=4.5(cm2)
結果は同じになりますが、これは根拠が明らかにおかしいです。算数の担当者としてこれに対して○をあげることはできません。
部分が誤りなのですが、もし正しいならば、角度が2倍なら高さも2倍(結果として面積も2倍)、角度が1/3倍なら高さも1/3倍(結果として面積も1/3倍)、が成り立たないといけないことになります。が、それがおかしいことはちょっと自分で作図してみると気づくはずです。
ひとつの問題を様々な方法で解いてみることは大切です。そのためには解説に書かれていることをなぞるだけでなく、自らの意思、ひらめきが必要な場合もあるでしょう。ですが、その時点ではあくまで「可能性」であり.それを検証する必要があるのです(自分だけでできない場合はそれこそ質問してみましょう)。「思いつき」は大切ですが「思い込み」はあってはいけないのです。
残りの日々を有効に活用して合格をつかみ取りましょう!

