2018年の灘中学の問題です。
「4個の整数,a,b,c,dがあり,bはaより1大きく,cはbより1大きく,dはcより1大きいです。a×b+b×c+c×d+d×aを計算すると2400になるとき,aは□です。」
ある程度算数の得意な中学受験生でもこの問題はなかなか解きにくいのではないでしょうか。
この問題は中学数学で学習する因数分解という考え方を使うと比較的楽に解けます。
因数分解とは、かんたんに言うと分配法則をつかって( )でくくるなどして、積の式をつくることです。
a×b+b×c+c×d+d×a
の式の下線部に注目すると、かっこでくくれます(分配法則)ので、
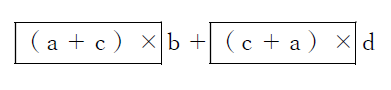
となります。さらに四角で囲んだ部分は共通なのでさらにかっこでくくれます。
(a+c)×(b+d)
となりますね。このあとは、aを求める問題なので、aを①とおくと、b=①+1、c=①+2、d=①+3 となりますから
(② +①+2)×(①+1+①+3)=(②+2)×(②+4)=2400
(②+2)と(②+4)は差が2なので、2400の約数で差が2のものを考えると、
48と50ですから、
②+2=48
となり、②=46ですから、①=23、すなわちa=23と求めることができます。
ところで、かけ算を長方形の面積で考えるクセがついていれば、
「a×b+b×c+c×d+d×a」
という式は4つの長方形の面積の合計と考えることができますね。
つまりこの式はたてa(cm)よこb(cm)の長方形と,たてb(cm)よこc(cm)の長方形と、たてc(cm)よこd(cm)の長方形と,たてd(cm)よこa(cm)の長方形の面積の合計を表しているわけです。
ここでこの4つの長方形を組み合わせて大きな長方形をつくると、たてが(a+c)(cm),よこが(b+d)(cm)の長方形になりますね。よって、
a×b+b×c+c×d+d×a=(a+c)×(b+d)
となる訳です。

